La Euroliga está parada debido a la pandemia de la COVID-19 y no se sabe qué ocurrirá con lo que queda de temporada. El Anadolu Efes estaba intratable y hasta ocho equipos estaban luchando por los últimos tres puestos de Playoffs. ¿Cómo podríamos predecir qué hubiese ocurrido si hubiese seguido la competición?
En mi última entrada describí cómo utilizar el sistema de puntuación Elo para cuantificar la calidad de los equipos de Euroliga a lo largo de la historia. En esta segunda entrada, voy a describir cómo simular el resto de partidos que quedan de temporada, incluyendo Playoffs y Final Four, utilizando esta puntuación.
Como ya expliqué, el sistema de puntuación Elo produce para cada partido una probabilidad de victoria esperada basada en la diferencia de las puntuaciones Elo de los dos equipos antes del partido. Pues bien, esta probabilidad es la que nos ayudará a elegir un ganador en cada encuentro de la simulación.
Nótese que las predicciones que voy a realizar son probabilísticas, no determinísticas. Esto es, el resultado de estas simulaciones será en forma de frecuencias relativas tras un gran número de simulaciones.
Simulación
La simulación comenzará con las puntuaciones Elo de los equipos al acabar la última jornada disputada de esta temporada (Jornada 28). El ganador de cada partido será elegido según la probabilidad esperada de victoria y las puntuaciones Elo serán actualizadas según este resultado.
Para poder actualizar las puntuaciones Elo en base a los resultados simulados deberemos de estimar la diferencia de puntos en el marcador al acabar el partido. Esto es debido a que el sistema Elo que utilicé también tiene en cuenta el márgen de victoria para actualizar las puntuaciones. Así pues, he construido un simple modelo Bayesiano de regresión para predecir la diferencia de puntos en el marcador en base a la diferencia de puntos Elo. Más adelante explico todas las suposiciones de este modelo en detalle.
Es importante recalcar que el ganador en un partido determinado no es determinístico, sino que se elige según unas probabilidades. Así pues, si repetimos la simulación una segunda vez, es posible que no obtengamos el mismo resultado. Esto es bueno ya que refleja la incertidumbre existente y nos permite explorar muchos escenarios diferentes. Por este motivo, realizaremos 1000 simulaciones de lo que queda de temporada y mostraremos los resultados finales.
1. Puntuaciones Elo iniciales
La siguiente tabla contiene el ranking de los equipos hasta esta ronda según la puntuación Elo. Lo primero que salta a la vista es que el Real Madrid es primero a pesar de que Anadolu Efes Istambul tiene dos victorias más. Otro equipo que sale mejor parado de esta clasificación Elo es el Zalgiris. Según la puntuación Elo, el equipo lituano está en séptima posición, mientras que en la clasificación actual estaría fuera de Playoffs en novena posición.
| Pos | Equipo | Elo |
|---|---|---|
| 1 | Real Madrid | 1717 |
| 2 | Anadolu Efes Istanbul | 1713 |
| 3 | CSKA Moscow | 1697 |
| 4 | FC Barcelona | 1625 |
| 5 | Maccabi FOX Tel Aviv | 1560 |
| 6 | Fenerbahce Beko Istanbul | 1538 |
| 7 | Zalgiris Kaunas | 1508 |
| 8 | Panathinaikos OPAP Athens | 1471 |
| 9 | Khimki Moscow Region | 1443 |
| 10 | Olympiacos Piraeus | 1443 |
| 11 | Valencia Basket | 1433 |
| 12 | KIROLBET Baskonia Vitoria-Gasteiz | 1415 |
| 13 | Crvena Zvezda mts Belgrade | 1400 |
| 14 | AX Armani Exchange Milan | 1398 |
| 15 | ALBA Berlin | 1370 |
| 16 | FC Bayern Munich | 1299 |
| 17 | LDLC ASVEL Villeurbanne | 1284 |
| 18 | Zenit St Petersburg | 1271 |
2. Modelo para la diferencia de puntos
Anteriormente mencioné que era necesario estimar la diferencia de puntos al final de cada encuentro que simulamos para poder actualizar las puntuaciones Elo. Para esto, podemos ajustar un modelo de regresión a los datos que tenemos de todas las temporadas anteriores.
El modelo nos permitirá predecir la diferencia de puntos en el marcador al acabar un partido basado en la diferencia en las puntuaciones Elo previas al partido. Utilizaremos un modelo Bayesiano para incluir toda la incertidumbre en torno a los parámetros del modelo y así incluirla en las simulaciones de los partidos.
Formalmente, si \(y_i\) es la diferencia de puntos entre el equipo local y el visitante en el partido \(i\) y \(x_i\) es la diferencia en la puntuación Elo entre el equipo local y el visitante (teniendo en cuenta el factor cancha), el modelo que utilizaremos para estimar el margen de victoria en cada partido simulado es el siguiente:
\[\begin{aligned} y_i &\sim \text{Normal}(\mu_i, \sigma^2) \\ \mu_i &= \alpha + \beta x_i \\ \alpha &\sim \text{Normal}(0, 1) \\ \beta &\sim \text{Log-Normal}(-4, 0.8) \\ \sigma &\sim \text{Uniform}(0, 50) \end{aligned}\]
He elegido estas distribuciones de probabilidad a priori realizando simulaciones predictivas a priori. A continuación podemos ver 50 lineas correspondientes al predictor lineal \(\mu_i\) obtenidas mediante simulaciones predictivas de las distribuciones a priori de \(\alpha\) y \(\beta\):
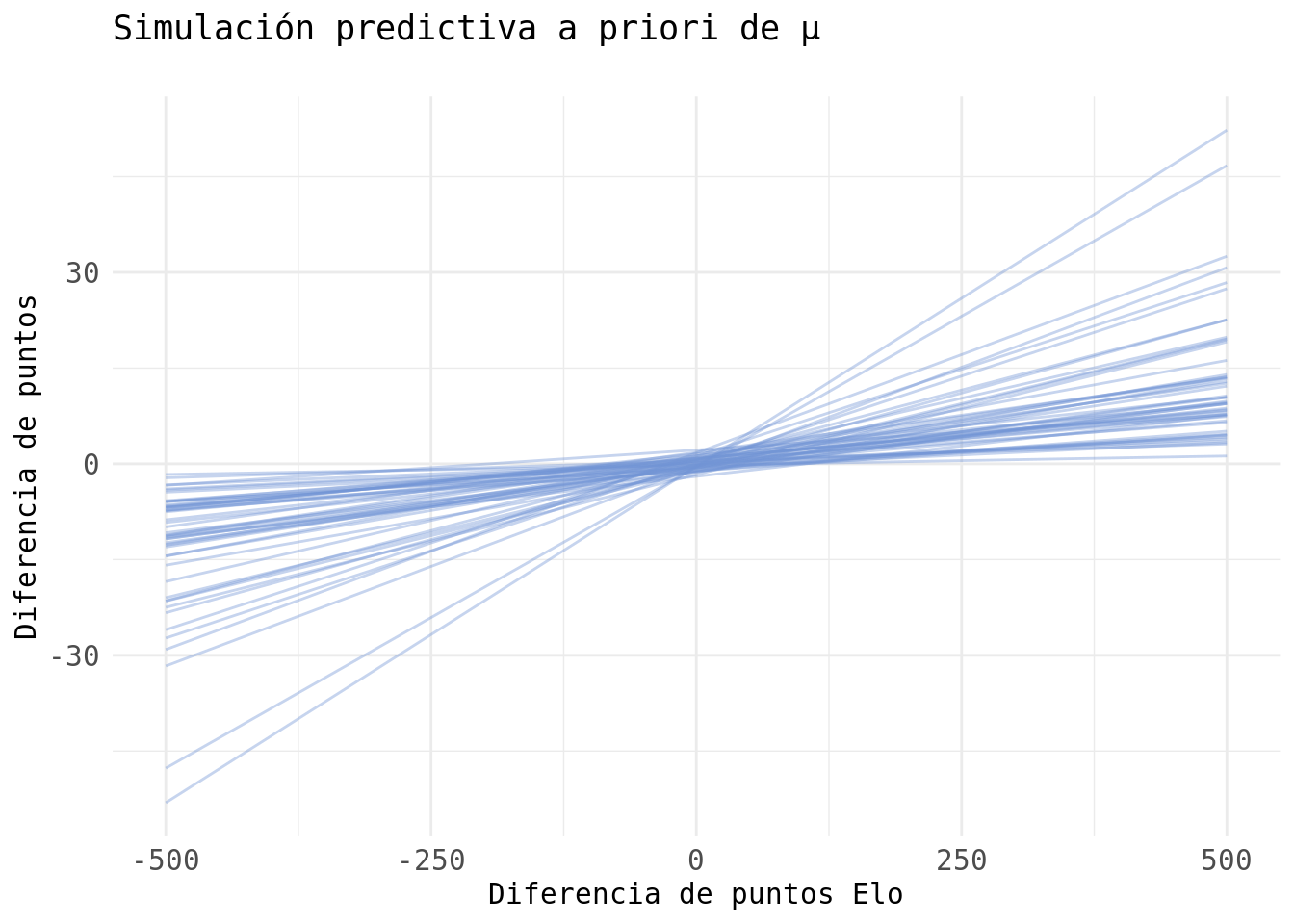
Es fácil entender el porqué de las distribuciones a priori de los parámetros \(\beta\) y \(\alpha\). En este caso \(\alpha\) representa la diferencia de puntos en el marcador cuando los dos equipos tienen la misma puntuación Elo antes de comenzar el partido (teniendo en cuenta el factor cancha). Esta diferencia de puntos debería estar alrededor de cero y por esto asignamos una distribución Normal con media 0 a \(\alpha\).
Por otro lado, \(\beta\) representa la pendiente del predictor lineal \(\mu_i\). No tiene sentido que esta pendiente sea negativa. Para ver esto, supón que tenemos a un buen equipo con una puntuación Elo de 1700. Con \(\beta < 0\) este equipo tendería a perder contra equipos peores que éste y además, perdería de un mayor margen cuanto peor fuera el rival. Obviamente esto es absurdo y por esto he asignado una distribución Log-Normal a \(\beta\).
Ahora procedemos a obtener la distribución a posteriori condicionando las distribuciones de probabilidad a priori a los datos. Utilizaremos aproximación cuadrática para esta tarea. Es posible implementar esta técnica en unas pocas líneas de código en R. En otra entrada explicaré en detalle en qué consiste este métdodo y por qué funciona para aproximar la distribución a posteriori.
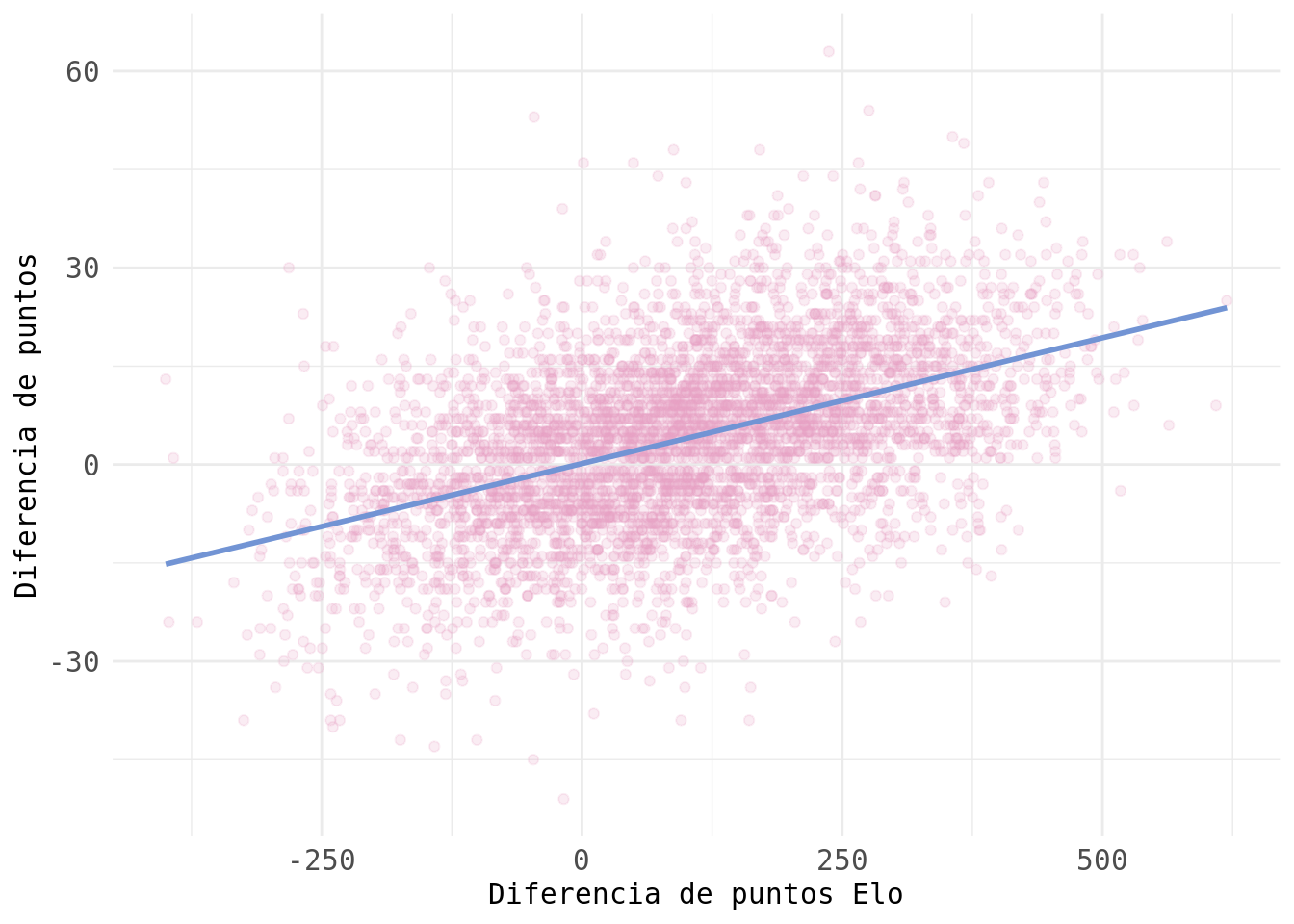
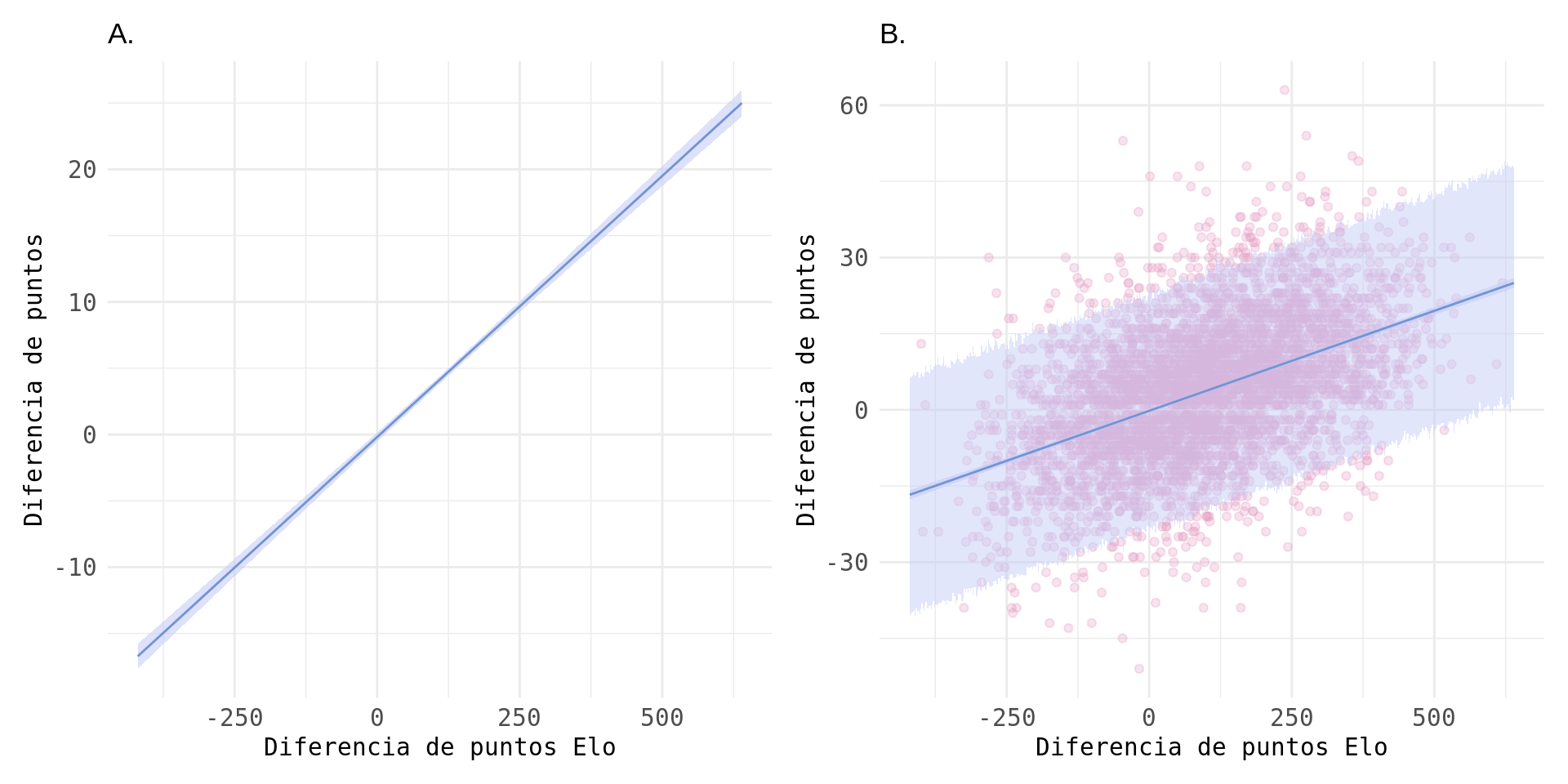
A continuación muestro la línea de regresión media obtenida con un intervalo de plausibilidad del 90% (A) y el intervalo de predicción del 90% de la distribución a posteriori (B). Vease que la incertidumbre de nuestro modelo con respecto a la línea de regresión es poca mientras que la incertidumbre en torno a las observaciones de diferencias de puntos es mucho mayor.
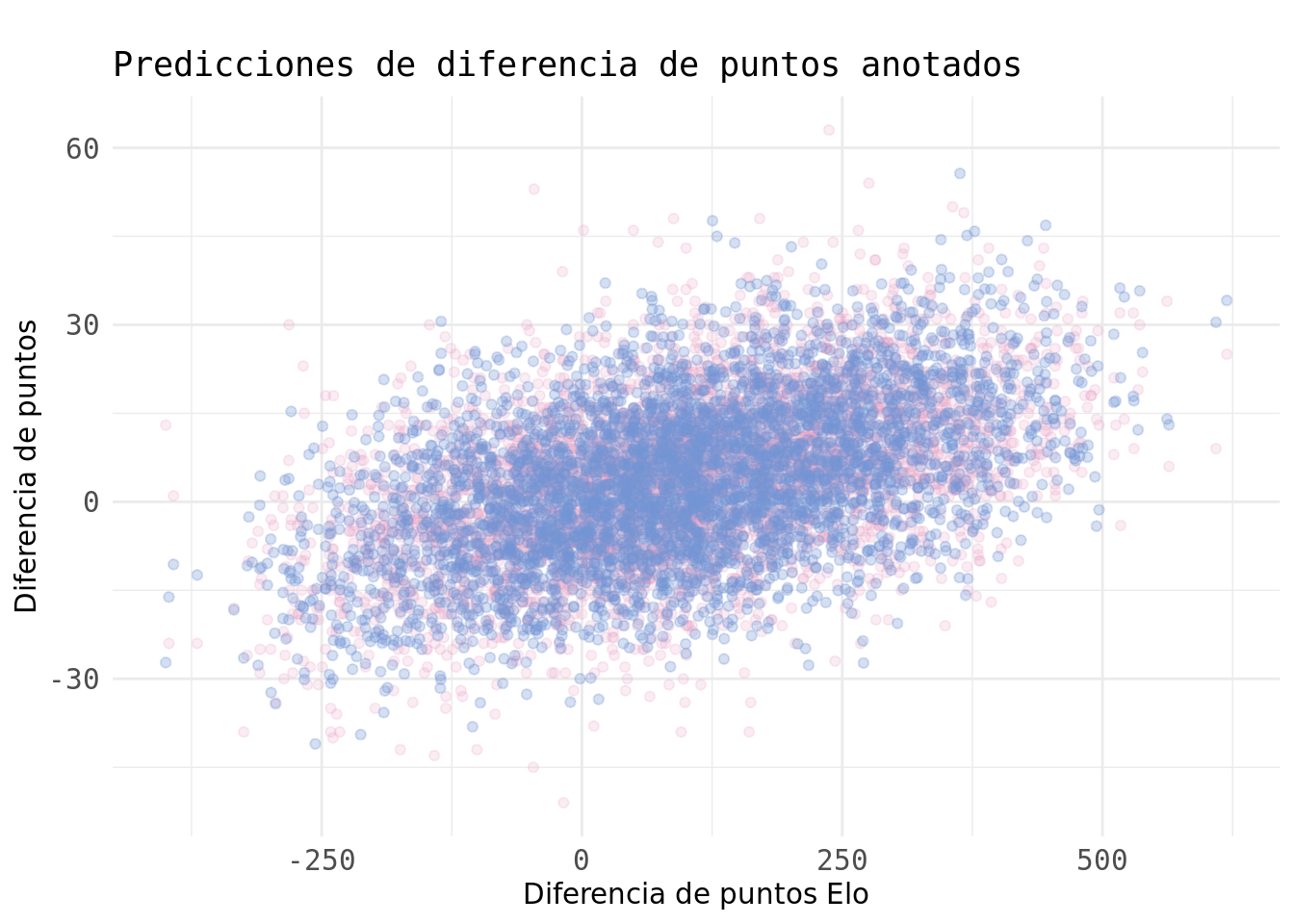
El siguiente gráfico muestra las diferencias en puntos predecidas por este modelo (azul) según las diferencias en puntos Elo observadas en los 4.425 partidos de nuestro conjunto de datos. Los puntos rojos corresponden a las diferencias observadas en realidad. Podemos observar que el modelo genera predicciones similares a las observadas.
3. Resultados
Queremos incorporar toda esta incertidumbre en las simulaciones de los partidos. Así pues, en cada partido este modelo generará una nueva observación de la diferencia de puntos en el marcador, que utilizaremos en nuestra simulación para decidir qué equipo gana el partido.
Dada la naturaleza probabilística del modelo, cada simulación de lo que resta de Euroliga resultará en uno de los muchos escenarios posibles. Lo que haré pues es realizar un gran número de simulaciones y ver qué escenarios son más frecuentes. Dado el gran número de escenarios posibles serán necesarias miles de simulaciones para obtener unas frecuencias relativas estables.
Estas frecuencias relativas pueden interpretarse como la probabilidad de que un escenario determinado ocurra. Así pues, he calculado, para todos los equipos, las probabilidades según este modelo de que este se clasifique para Playoffs, de que se clasifique para la Final 4, de que llegue a la final y de ser campeón. A continuación muestro estas probabilidades tras 10.000 ligas simuladas.
| Equipo | Elo | Playoffs | Final 4 | Final | Campeón |
|---|---|---|---|---|---|
| Anadolu Efes Istanbul | 1713 | 100.00% | 91.84% | 51.64% | 28.74% |
| Real Madrid | 1717 | 100.00% | 68.44% | 40.51% | 21.33% |
| CSKA Moscow | 1697 | 100.00% | 73.63% | 36.35% | 20.18% |
| FC Barcelona | 1625 | 100.00% | 72.46% | 33.57% | 14.28% |
| Maccabi FOX Tel Aviv | 1560 | 100.00% | 28.19% | 10.88% | 4.66% |
| Fenerbahce Beko Istanbul | 1538 | 67.55% | 21.15% | 9.36% | 3.84% |
| Panathinaikos OPAP Athens | 1471 | 75.48% | 16.73% | 6.87% | 2.75% |
| Khimki Moscow Region | 1443 | 51.51% | 10.07% | 3.91% | 1.63% |
| AX Armani Exchange Milan | 1398 | 25.81% | 5.37% | 2.18% | 0.85% |
| Zalgiris Kaunas | 1508 | 27.22% | 4.52% | 1.92% | 0.70% |
| Olympiacos Piraeus | 1443 | 19.99% | 3.75% | 1.41% | 0.56% |
| Crvena Zvezda mts Belgrade | 1400 | 6.49% | 1.16% | 0.49% | 0.19% |
| KIROLBET Baskonia Vitoria-Gasteiz | 1415 | 9.63% | 1.19% | 0.48% | 0.18% |
| Valencia Basket | 1433 | 16.27% | 1.48% | 0.41% | 0.10% |
| ALBA Berlin | 1370 | 0.04% | 0.02% | 0.02% | 0.01% |
| LDLC ASVEL Villeurbanne | 1284 | 0.01% | 0.00% | 0.00% | 0.00% |
| FC Bayern Munich | 1299 | 0.00% | 0.00% | 0.00% | 0.00% |
| Zenit St Petersburg | 1271 | 0.00% | 0.00% | 0.00% | 0.00% |