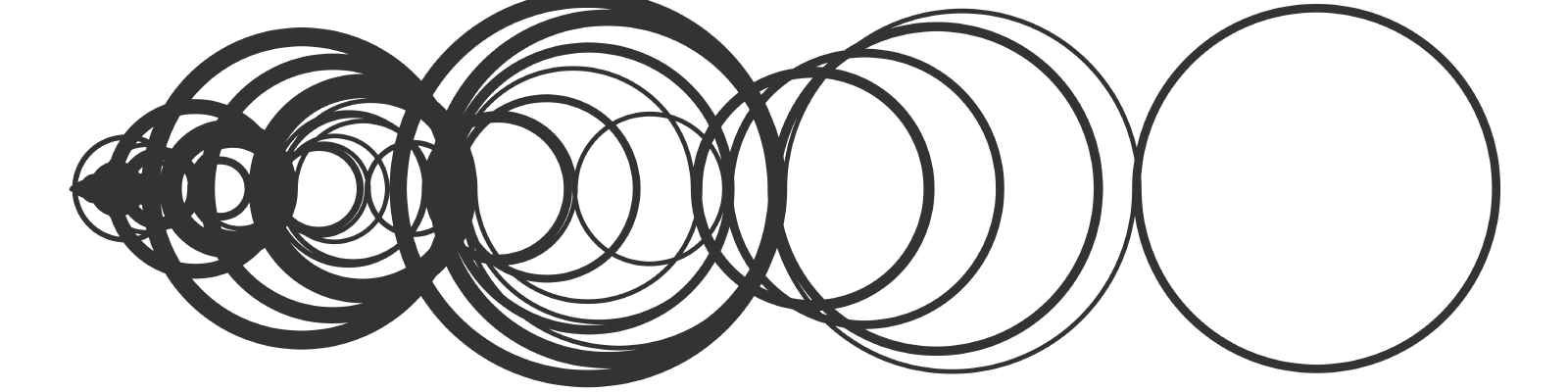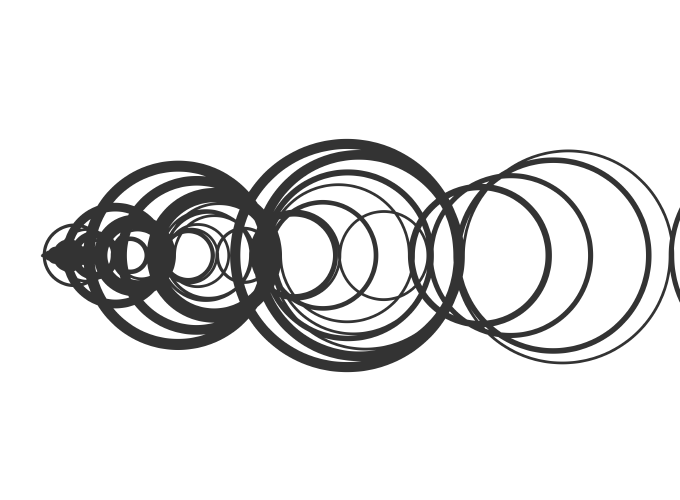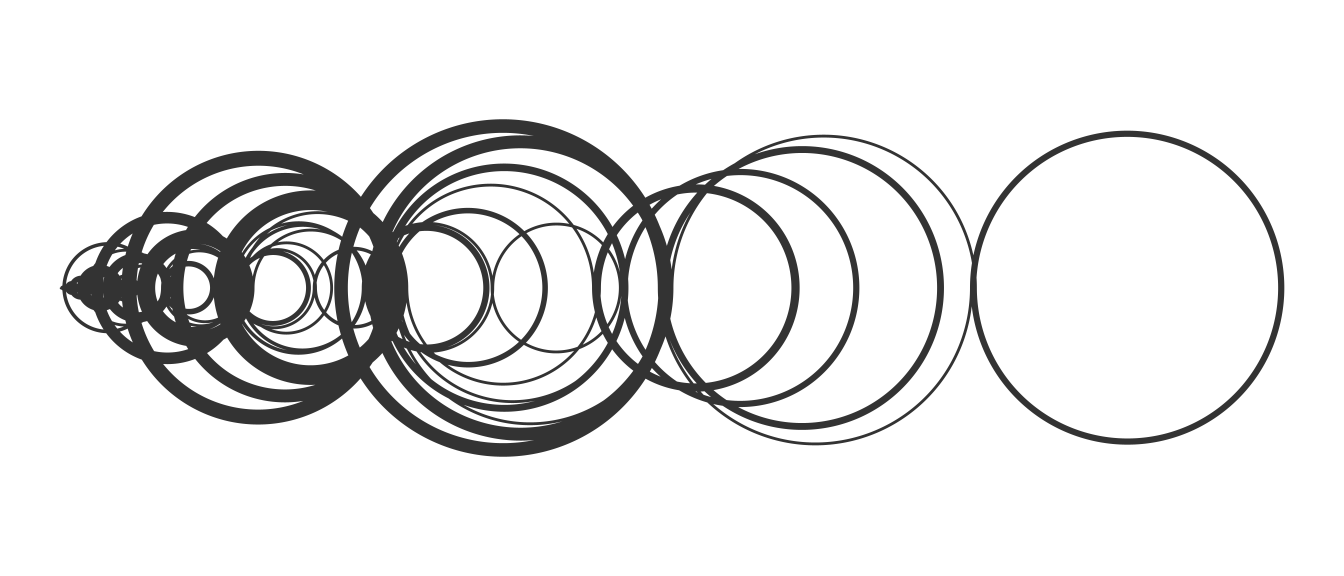Échale un ojo a la siguiente secuencia de números:
\[0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, \ldots\]
Si no la has visto nunca, seguramente no consigas averiguar qué patrón sigue esta secuencia. Se trata de la llamada secuencia de Recamán, atribuída al matemático colombiano Bernardo Recamán.
A pesar de su aparente complejidad, las reglas para generar esta secuencia son más bien sencillas. Lo mejor para comprender el algoritmo que genera esta secuencia es dibujar una línea que vaya desde 0 hasta, por ejemplo, 7 para empezar: 
Básicamente se trata de, empezando desde el \(0\), en cada paso intentamos ir hacia la izquierda un número de unidades igual al paso en el que nos encontramos. Si el número en el que caemos al ir a la izquierda está a la izquierda de \(0\) o ya ha aparecido en nuestra secuencia anteriormente, en lugar de ir a la izquierda vamos a la derecha.
El escritor Alex Bellos lo explica mucho mejor en el siguiente vídeo de Numberphile:
Implementación en R
Para esta entrada he utilizado R para generar y dibujar la secuencia de Recamán. En unas pocas líneas de código podemos crear una función que genere un número determinado de elementos de esta secuencia:
# Generar los primeros n números de la secuencia de Recamán
get_recaman <- function(n) {
recaman_seq <- numeric(n)
for (i in 1:length(recaman_seq)) {
candidate <- recaman_seq[i] - i
if (candidate > 0 & !(candidate %in% recaman_seq)) {
recaman_seq[i + 1] <- candidate
} else recaman_seq[i + 1] <- recaman_seq[i] + i
}
recaman_seq <- recaman_seq[-length(recaman_seq)]
recaman_seq
}
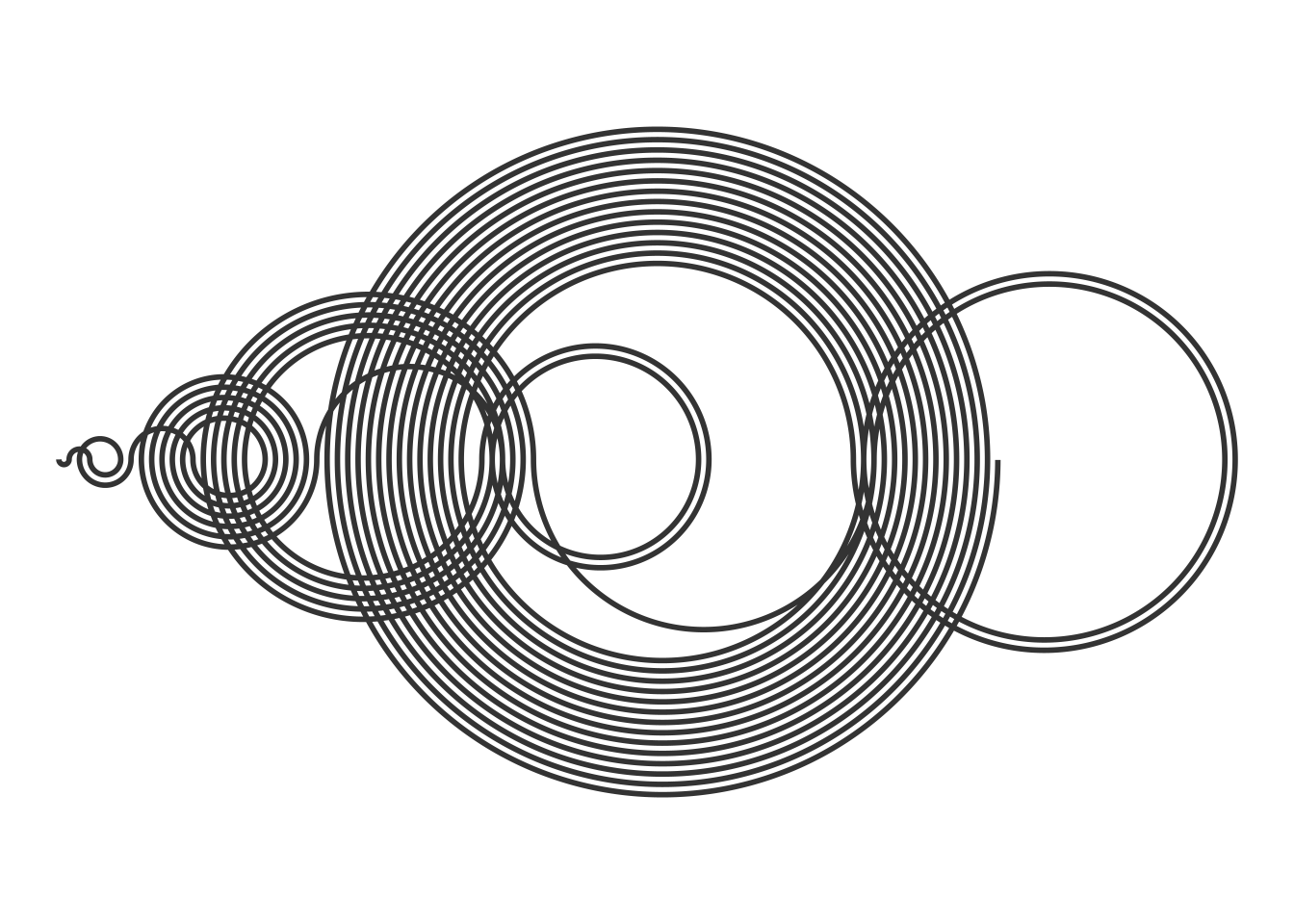
get_recaman(20)## [1] 0 1 3 6 2 7 13 20 12 21 11 22 10 23 9 24 8 25 43 62Para dibujar la secuencia utilizamos semicírculos que representen los saltos de un número al otro.
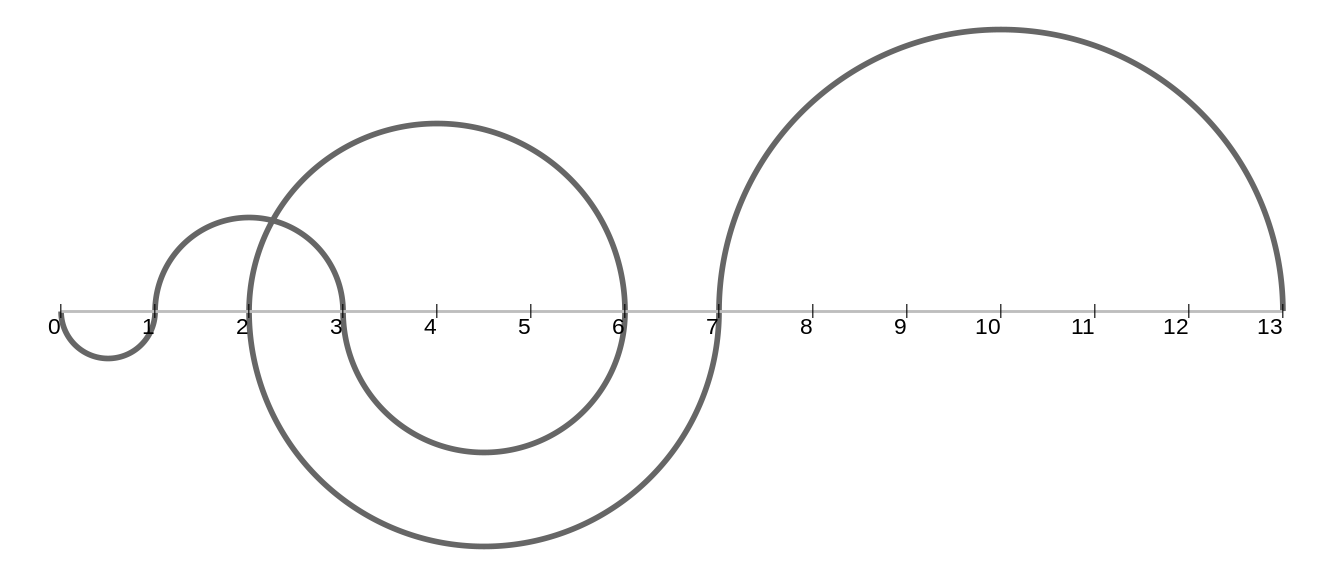
Puedes obtener el código para dibujar la secuencia aquí.