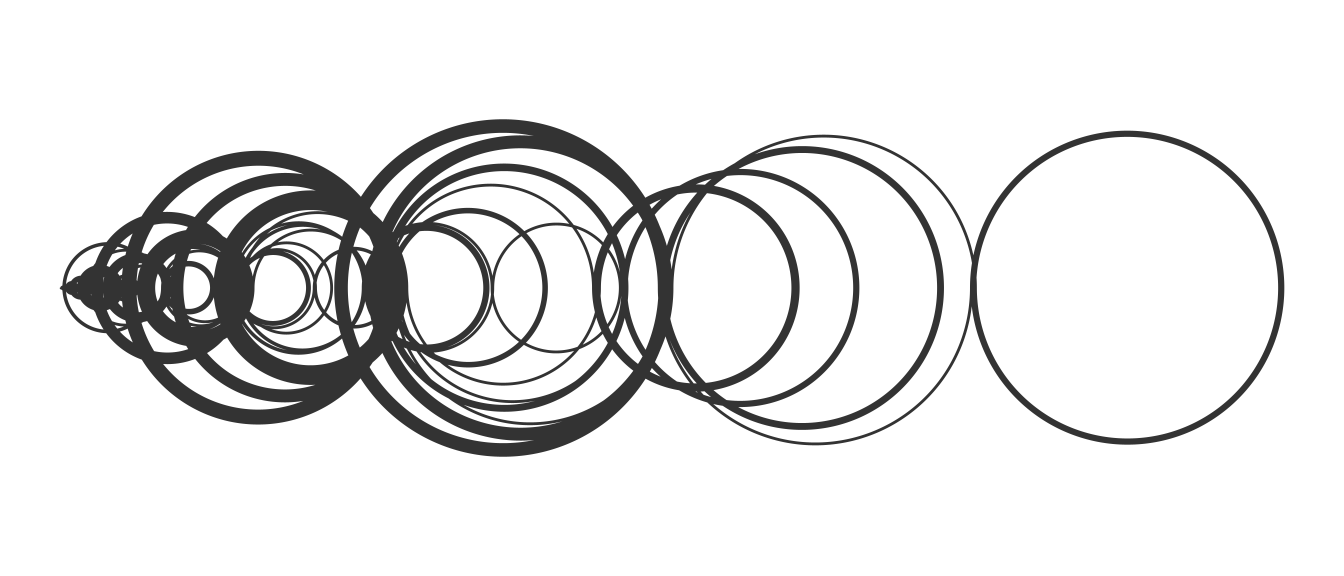Take a look at the following sequence of numbers:
If you have not seen it before, you probably will not be able to figure out the pattern in this sequence. It is the so called Recamán’s sequence, attributed to the Colombian mathematician Bernardo Recamán.
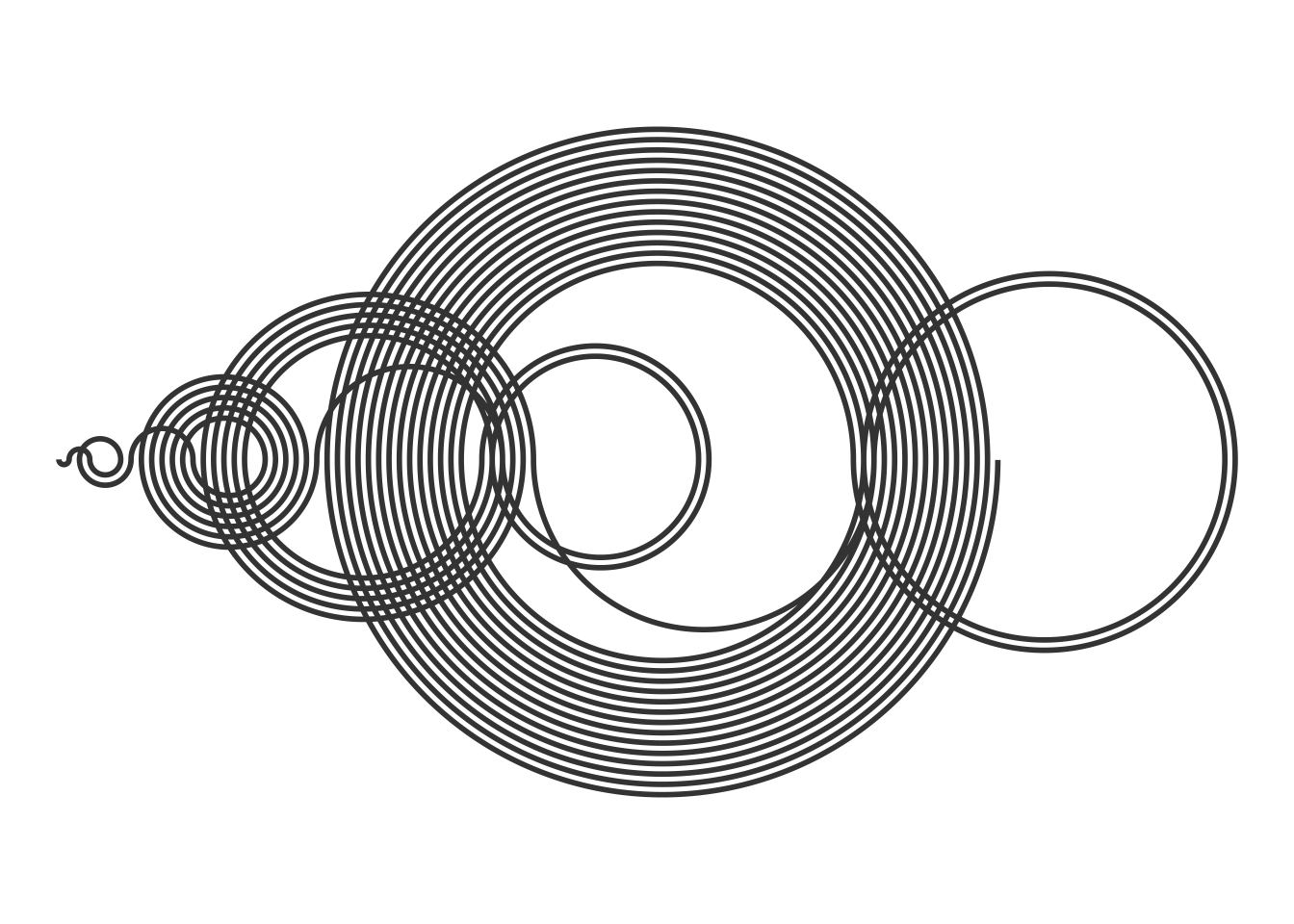
Despite its apparent complexity, the rules that generate this sequence are quite simple. The best way to understand the generating algorithm is to draw the number line from 0 to, say, 7 to start:
Basically, starting from , in each step we try to move left by a number of units equal to the step we are taking. If the number in which we land is to the left of zero or it has already appeared before in our sequence, instead of moving left we move right.
The writer Alex Bellos explains it much better in the following video of Numberphile:
Implementation in R
For this blog post I have used R to generate and draw the Recamán sequence. In a few lines of code we can create a function that generates a given number of elements of this sequence:
# Generate the first n numbers of the Recamán sequence
get_recaman <- function(n) {
recaman_seq <- numeric(n)
for (i in 1:length(recaman_seq)) {
candidate <- recaman_seq[i] - i
if (candidate > 0 & !(candidate %in% recaman_seq)) {
recaman_seq[i + 1] <- candidate
} else recaman_seq[i + 1] <- recaman_seq[i] + i
}
recaman_seq <- recaman_seq[-length(recaman_seq)]
recaman_seq
}
get_recaman(20)## [1] 0 1 3 6 2 7 13 20 12 21 11 22 10 23 9 24 8 25 43 62To draw the sequence we use semicircles that represent the jumps from one number to the other.
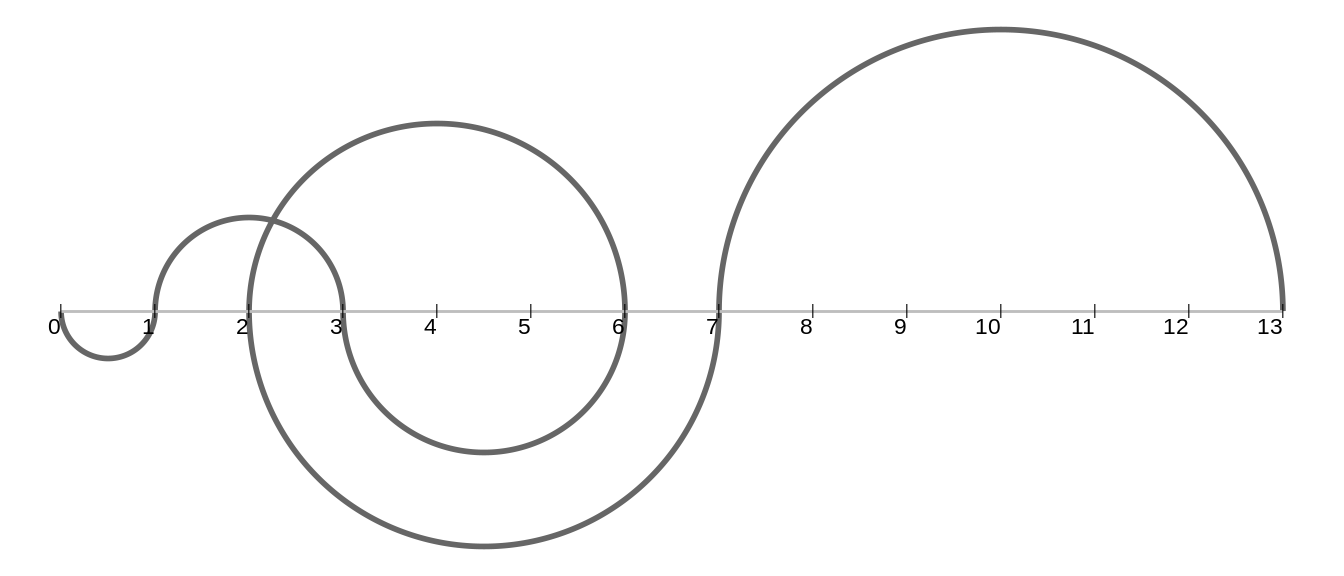
Yo can find the code to draw the sequence here.
Exploring Recaman’s path
Play around with the code and explore the sequence. Do you think that every integer eventually appears? It is conjectured that no, that there are holes along Recamán’s path.